Binary Search Guide

Recently, the LeetCode daily problems frequently focus on topics of binary search. so I update this note, include and share them.

Note: The following content is a collection of tutorials from leetcode. I’m not the original author; I have simply organized the material for easier access and study.

When to use Binary Search?

Every time you need to search for an index or element in a collection. If the collection is unordered, we can always sort it first before applying Binary Search.

User Guide for Binary Search

Reference

• Python Powerful Ultimate Binary Search Template. Solved many problems
• Binary Search 101

Binary search is often a topic that’s easy to be explained on the abstract level, but when it comes to writing bug free implementations, it’s rather difficult.

Some of the most common problems include:

1. Infinity loop
2. Can’t decide where to shrink
3. Do I use lo or hi
4. When to exit the loop
5. …

In this article, I will be sharing my insights on how to write bug free binary search with just a little pattern.

If you are familiar with binary search and just want to see the pattern, you can go directly to the part: The Pattern.

What is binary search?

Normally, to find the target in a group, such as an array of numbers, the worst case scenario is we need to go through every single element (O(n)). However, when these elements are sorted, we are able to take the privilege of this extra information to bring down the search time to $\mathcal{O}(logn)$, that is if we have 100 elements, the worst case scenario would be 10 searches. That is a huge performance improvement.

The Gif below demonstrates the power of binary search.

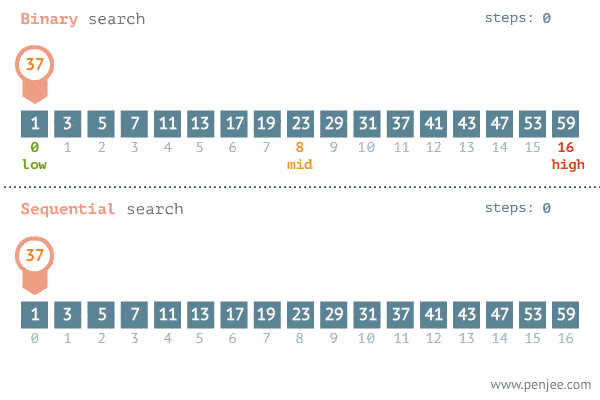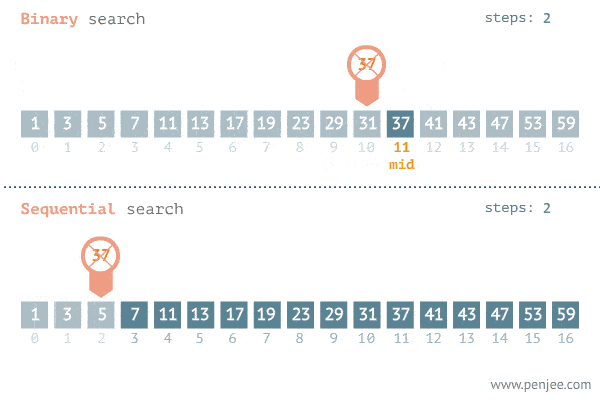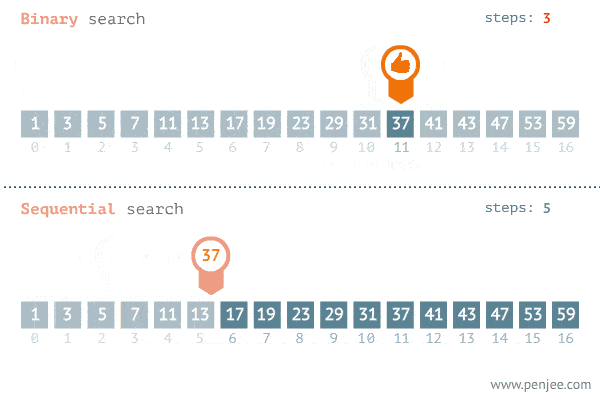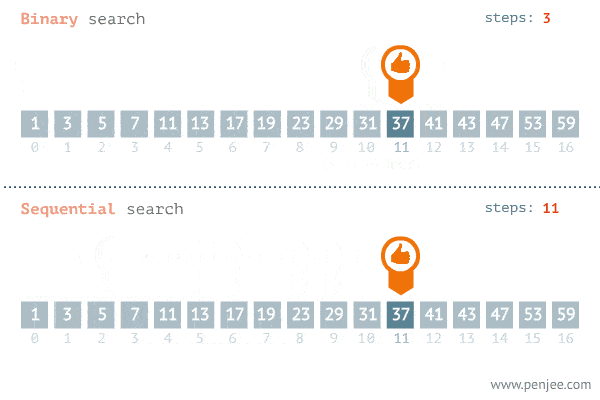
The reason behind this huge performance increase is because for each search iterations, we are able to cut the elements we will be looking at in half. Fewer elements to look at = faster search time. And this all comes from the simple fact that in a sorted list, everything to the right of n will be greater or equal to it, and vice versa.

Before we look at the abstract ideas of binary search, let’s see the code first:

var search = function(nums, target) {
    let lo = 0, hi = nums.length-1;
    while (lo < hi) {
        let mid = lo + Math.floor((hi-lo+1)/2);
        if (target < nums[mid]) {
            hi = mid - 1
        } else {
            lo = mid; 
        }
    }
    return nums[lo]==target?lo:-1;
};

The fundamental idea

1. lo & hi

We define two variables, let’s call them lo and hi . They will store array indexes and they work like a boundary such that we will only be looking at elements inside the boundary.
Normally, we would want initialize the boundary to be the entire array.

let lo = 0, hi = nums.length-1;

2. mid

The mid variable indicates the middle element within the boundary. It separates our boundary into 2 parts. Remember how I said binary search works by keep cutting the elements in half, the mid element works like a traffic police, it indicates us which side do we want to cut our boundary to.

Note when an array has even number of elements, it’s your decision to use either the left mid (lower mid) or the right mid (upper mid)

let mid = lo + Math.floor((hi - lo) / 2); // left/lower mid

let mid = lo + Math.floor((hi - lo + 1) / 2); // right/upper mid

3. Comparing the target to mid

By comparing our target to mid, we can identify which side of the boundary does the target belong. For example, If our target is greater than mid, this means it must exist in the right of mid . In this case, there is no reason to even keep a record of all the numbers to its left. And this is the fundamental mechanics of binary search - keep shrinking the boundary.

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

4. Keep the loop going

Lastly, we use a while loop to keep the search going:

while (lo < hi) { ... }

The while loop only exits when lo == hi, which means there’s only one element left. And if we implemented everything correctly, that only element should be our answer(assume if the target is in the array).

The pattern

It may seem like binary search is such a simple idea, but when you look closely in the code, we are making some serious decisions that can completely change the behavior of our code.
These decisions include:

1. Do I use left or right mid?
2. Do I use < or <= , > or >=?
3. How much do I shrink the boundary? is it mid or mid - 1 or even mid + 1 ?
4. …

And just by messing up one of these decisions, either because you don’t understand it completely or by mistake, it’s going to break your code.
To solve these decision problems, I use the following set of rules to always keep me away from trouble, most importantly, it makes my code more consistent and predictable in all edge cases.

1. Choice of lo and hi, aka the boundary

Normally, we set the initial boundary to the number of elements in the array

let lo = 0, hi = nums.length - 1;

But this is not always the case.
We need to remember: the boundary is the range of elements we will be searching from.
The initial boundary should include ALL the elements, meaning all the possible answers should be included. Binary search can be applied to none array problems, such as Math, and this statement is still valid.

For example, In LeetCode 35, the question asks us to find an index to insert into the array.
It is possible that we insert after the last element of the array, thus the complete range of boundary becomes

let lo = 0, hi = nums.length;

2. Calculate mid

Calculating mid can result in overflow when the numbers are extremely big. I ll demonstrate a few ways of calculating mid from the worst to the best.

let mid = Math.floor((lo + hi) / 2) // worst, very easy to overflow

let mid = lo + Math.floor((hi - lo) / 2) // much better, but still possible

let mid = (lo + hi) >>> 1 // the best, but hard to understand

When we are dealing with even elements, it is our choice to pick the left mid or the right mid , and as I ll be explaining in a later section, a bad choice will lead to an infinity loop.

let mid = lo + Math.floor((hi - lo) / 2) // left/lower mid

let mid = lo + Math.floor((hi - lo + 1) / 2) // right/upper mid

3. How do we shrink boundary

I always try to keep the logic as simple as possible, that is a single pair of if...else. But what kind of logic are we using here? My rule of thumb is always use a logic that you can exclude mid.
Let’s see an example:

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

Here, if the target is less than mid, there’s no way mid will be our answer, and we can exclude it very confidently using hi = mid - 1. Otherwise, mid still has the potential to be the target, thus we include it in the boundary lo = mid.
On the other hand, we can rewrite the logic as:

if (target > nums[mid]) {
	lo = mid + 1; // mid is excluded
} else {
	hi = mid; // mid is included
}

4. while loop

To keep the logic simple, I always use

while(lo < hi) { ... }

Why? Because this way, the only condition the loop exits is lo == hi. I know they will be pointing to the same element, and I know that element always exists.

5. Avoid infinity loop

Remember I said a bad choice of left or right mid will lead to an infinity loop? Let’s tackle this down.
Example:

let mid = lo + ((hi - lo) / 2); // Bad! We should use right/upper mid!

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

Now, imagine when there are only 2 elements left in the boundary. If the logic fell into the else statement, since we are using the left/lower mid, it’s simply not doing anything. It just keeps shrinking itself to itself, and the program got stuck.
We have to keep in mind that, the choice of mid and our shrinking logic has to work together in a way that every time, at least 1 element is excluded.

let mid = lo + ((hi - lo + 1) / 2); // Bad! We should use left/lower mid!

if (target > nums[mid]) {
	lo = mid + 1; // mid is excluded
} else {
	hi = mid; // mid is included
}

6. When you must set lo <= hi?

If we return lo after while loop and set with lo < hi, there’s the problem: at last lo == hi but we never compute them in while loop, which means we never check the validation of lo index. If we have to check, we have to make lo == hi to continue the check. There’s another sign: if we return mid during the loop, we can set lo <= hi.

So when your binary search is stuck, think of the situation when there are only 2 elements left. Did the boundary shrink correctly?

Summary

My rule of thumb when it comes to binary search:

1. Include ALL possible answers when initialize lo & hi
2. Don’t overflow the mid calculation
3. Shrink boundary using a logic that will exclude mid
4. Avoid infinity loop by picking the correct mid and shrinking logic
5. Always think of the case when there are 2 elements left

Because this problem is a failrly easy, the implementions may be pretty straight forward and you may wonder why do I need so many rules. However, binary search problems can get much much more complex, and without consistent rules, it’s very hard to write predictable code. In the end, I would say everybody has their own style of binary serach, find the style that works for you!

Problems

• [[704. Binary Search]]
• [[69. Sqrt(x)]]
• [[33. Search in Rotated Sorted Array]]
• 1552. Magnetic Force Between Two Balls
• 1482. Minimum Number of Days to Make m Bouquets
• 826. Most Profit Assigning Work
• 633. Sum of Square Numbers